Expanding The Logical Foundations Of The Quranc (Part 4)

The Unity of Logic: From Atomic Quantification to Divine Names

I. The Foundation of Atomic Quantification

The synthesis of logical rules with concrete concepts requires more than just the four laws of thought and their associated rules of replacement. We must employ judgment functions—what modern logic terms quantifiers. Atomic quantification, at its core, represents our ability to determine specific conditions recursively.

Consider the concept of "vehicle." When we recognize vehicular systems in biology (nutrient transport) or economics (resource movement), we're engaging in direct quantificational application. This ability to apply concepts flexibly across domains stems from quantification's fundamental nature.

II. The Nature of Logical Self-Reference

The Paradox That Isn't

Self-reference in logic isn't problematic—it's essential to mind's function. As Kant noted:

"The conditions of the possibility of experience in general are at the same time conditions of the possibility of the objects of experience". Kant Critique of Pure Reason, A158/B197

This self-referential principle powered major breakthroughs like Leibniz and Newton's calculus. As Leibniz observed:

"This principle is not simply a law of nature; rather it is a universal law showing us how we are to find and to grasp natural laws" E. Cassirer 'Determinism & Indeterminism p159

III. The Calculus Connection

The calculus method illuminates this logical structure through three components:

1. Non-contradiction as the integral

2. Modus tollens as the constant

3. Atomic quantifier as the derivative

This triadic structure appears in diverse contexts:

In Physics and Mathematics

• Quantum mechanics' uncertainty principle

• Statistical mechanics' probability distributions

• The infinitesimal in calculus

In Natural Systems

The Quranic verse provides profound insight:

وَاللَّهُ خَلَقَ كُلَّ دَابَّةٍ مِّن مَّاءٍ ۖ فَمِنْهُم مَّن يَمْشِي عَلَىٰ بَطْنِهِ وَمِنْهُم مَّن يَمْشِي عَلَىٰ رِجْلَيْنِ وَمِنْهُم مَّن يَمْشِي عَلَىٰ أَرْبَعٍ

"And Allah has created from water every living creature (دَابَّةٍ - dabbah). Some of them crawl on their bellies, some walk on two legs, and some walk (يَمْشِي - yamshi) on four (أَرْبَعٍ - arba')" (An-Nur: 45)

The Hidden Logic of Four-Legged

Motion and Continuous Processes

Have you ever watched a horse in motion? There's something fascinating about how its legs move - when two legs are pushing off the ground, the other two are lifting up. This isn't just random coordination; it's a perfect example of nature's logic at work. The pattern follows one of the most basic principles of logic: two opposite states cannot exist in the same way at the same time. As the front legs push down, the back legs must lift up, and vice versa, creating a continuous, flowing motion.

Zeno's Race and the Nature of Continuity

Achilles can never quite catch up because the space between them is infinitely divisible - each time he reaches where the tortoise was, it has moved slightly ahead. But rather than seeing this as a problem, we can view it as revealing something profound about continuity itself. Like a horse's gait, it's not about reaching a final point but about the perpetual flow of motion.

Four Legs vs. Two: A Study in Continuous Motion

Consider the difference between four-legged and two-legged animals. A horse's gallop has a natural, unbroken flow that we humans, with our two-legged walk, can't quite match. Our walking requires constant balance and adjustment, while a horse's movement follows a more natural, continuous rhythm.

Beyond Movement: Continuity in Everyday Life

This principle of continuity shows up in surprising places:

1. Legal proceedings, where a witness's testimony gains strength through consistent maintenance over time

2. The experience of waiting - for a verdict, a job response, or even a class to end

3. Our perception of time itself, flowing endlessly forward

The Deeper Meaning

What appears at first as simple number (four legs) reveals itself as something more profound - a window into how nature organizes continuous processes. It's not just about counting legs; it's about understanding how natural systems maintain unbroken, self-sustaining patterns.

Through these examples - from horse gaits to ancient paradoxes to legal proceedings - we see how continuity isn't a limitation but a fundamental principle of how reality works. It's nature's way of maintaining unbroken, self-sustaining processes that form the fabric of our world.

More than that, we can read De morgan Laws in this scheme of 'four'

IV. Divine Names and Logical Structure

The divine name الوهاب (Al-Wahab, The Bestower) illustrates how consciousness of invocation provides deeper understanding. This relates to the concept of نعمة (Neema), which encompasses:

• Permanence

• Generativity

• Resourcefulness

• Developmental potential

  
  

The term عظيم (Adeem) denotes complexity in implications, particularly in how divine gifts manifest through multiple layers of meaning and application.

Understanding Solomon's Gifts: From Miracle to Necessity

When we examine Solomon's gifts - his ability to understand animal speech and command the winds - we must see them not as mere miraculous exceptions to natural law, but as necessary expressions of his essential nature as king. These abilities were not arbitrary additions but fundamental conditions of his specific mode of kingship.

Just as Kant shows that the conditions that make experience possible are the same conditions that make the objects of experience possible, Solomon's gifts were not simply added powers but the very conditions that made his particular form of kingship possible. His ability to understand animals and command winds were not exceptions to rules but were themselves rules within their own domain - as natural to his kingship as the use of transport animals is to human civilization.

This illustrates a broader principle about Quranic terms: to truly understand them, we must go beyond simple identity (A = A) to grasp how each concept contains its own conditions of possibility. We must establish what makes the concept what it is - its necessary conditions and relations - before we can understand it in its full, transcendental sense.

V. Synthesis: The Calculus of Logic

The cognitive structure underlying these concepts is logical before mathematical—qualitative before quantitative. Like coordinates in analytic geometry (x,y, z), it provides:

• A non-contradictory ground (integral)

• Rules governing behavior of elements (constant)

• Methods of application (derivative)

VI. Zeno's Paradox and Continuous Systems

Zeno's paradox of Achilles and the tortoise reveals fundamental truths about continuity. Rather than a limitation, it demonstrates:

• Self-contained, perpetual processes

• The nature of continuous movement

• The relationship between discrete and continuous phenomena

These principles reflect in both natural systems and divine wisdom, showing how logical structures underpin our understanding of both physical and metaphysical realities.

Q: Does Modus tollens mean more than the conventional definition gives?

A: Yes. While traditionally defined as the "mode of denying," modus tollens operates far more fundamentally. The conventional view states:

• If a statement is true, its consequence must be true

• If the consequence is false, the original statement must be false

• Example: If you're a dog, you're an animal. You're not an animal. Therefore, you're not a dog.

  
  

However, this merely scratches the surface.

Q: How does this denial actually function?

A: The denial works not as a rejection of the concept itself, but as a "general abdication." It's logic's method of:

• Determining the subject who determines

• Establishing conditions prior to any determination

• "Stripping away" conditions that would make a concept specific

  
  
  
  

Q: Why does this form a spectrum?

A: The denial creates a spectrum because:

• Modus tollens asserts the pre-assertive side

• The denial, while negating specific assertions, is itself an assertion

• This metalogical assertion enables us to conceive things in themselves

• It provides the abstraction needed to treat any concept as though it were the subject itself

  
  

Q: Why frame it in this seemingly paradoxical way?

A: It's a syntactic convention. The best explanation comes through denying any specific explanation. As Russell noted:

• False propositions imply all propositions

• True propositions are implied by all propositions

  Principles Of Mathematics, chp II, sec 18

  
  

This represents the first coherent articulation in what we might call the continuum dimension. Consider a trajectory of a car or plane - you see an uninterrupted straight line, a continuous moving forward. Remove all other ideas about what's moving, how fast, how it moves, what it's moving towards, and you obtain the idea of continuity itself.

Q: Can the rules of logic be shaped by the calculus method, and can the calculus be shaped by logic?

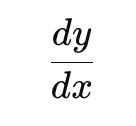
A: Yes, absolutely. The calculus is inherently logical; it represents logic applied to quantities:

• The logical aspect is the structure, given by notation and arrangement

• The mathematical aspect is the values obtained when applied to objects

• Following Leibniz's logical calculus, we can produce logical propositions with mathematical precision

  
  

The key insight is that our constants, integrals, and derivatives are actually conditions of knowledge itself—functioning as cognitive structures. They are, to use a modern analogy, like the "weights" in a neural network, determining nothing less than the rules of logic themselves.

In logic, our constants are rules of logic, more specifically, those more general rules that can be understood as ‘classes’ under which other rules fall, as such, in logic, constants are ‘real constants’ as opposed to ‘the general initial condition’ with which we usually start our mathematical calculations. while the calculus may be modelling some geometrical relation, the logical calculus is modelling the very cognitive framework that's modelling the geometrical relation, Here, modus tollen represent all constants obeying the structure of this rule, here all our elements behave in the manner denoted by the formula (-q → -p), that relation which in non-contradiction is presented in its pure form, call non contradiction simply that principle which emphasizes ‘difference in sense’ (as we showed earlier with the four-footed animal analogy), becomes the condition of the very objects with which our analysis deals, every object conceived under non contradiction is inferred as both possible as well as valid/real object, that is, the object is taken in its full sense. 

Hypothetical Syllogism and Universal Quantification

The Nature of Hypothetical Syllogism

A hypothetical syllogism makes mediate, indirect assertions. If Socrates is a man, and men are mortal, then Socrates is mortal. Similarly, if a hippopotamus is amphibious, we directly infer its adaptation for aquatic life based on what 'amphibian' involves.

The universal quantifier allows us to state anything predicable from a concept's underlying nature. In the idea of Man are contained all propositions generally true of, and unique to, man - known and unknown. These are 'assertable' and 'determinable' apriori through the universal quantifier, forming what Russell calls a "class of implications."

Quranic Applications

The Quran employs this concept through كل (Kul) and كلما (Kulama):

كُلَّمَا دَخَلَ عَلَيْهَا زَكَرِيَّا الْمِحْرَابَ وَجَدَ عِندَهَا رِزْقًا "Every time Zakaraya saw her, he saw that she was well-stocked" (3:37)

And:

كُلُّ ٱلطَّعَامِ كَانَ حِلًّۭ لِّبَنِىٓ إِسْرَٰٓءِيلَ "All food was lawful for the children of Israel". (6:5)

Here, كل represents a true quantifier (the arabic version of 'all' or 'every'. When applied to something like 'food', it indicates all potential types - the potentiality being intrinsic. This universality is subjective, restricted to individual experience rather than absolute universality.

Four Dimension

Four distinct dimensions arise as a result of the classificatory triadization the rules of logic.

The Continuum Dimension

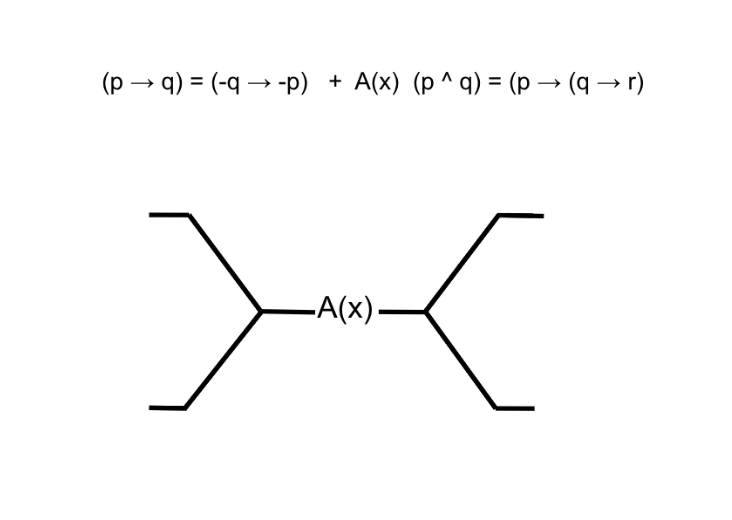
• Integral: Law of non-contradiction

• Constant: Modus Tollens

• Derivative: Atomic quantifier

The Discreteness Dimension

This dimension parallels the structure found in non-contradiction:

• Integral: Law of excluded middle

• Constant: Hypothetical syllogism

• Derivative: Universal quantifier

  
  

Objects here are embodiments of laws, not direct entities. Like the indeterminacy in our continuum dimension, this presents a challenge. We resolve it through generalization: all objects are embodiments of laws or orders. The integral is this generalization, the constancy is object behavior, and derivatives are our judgments of discreteness.

Monothetic Dimension

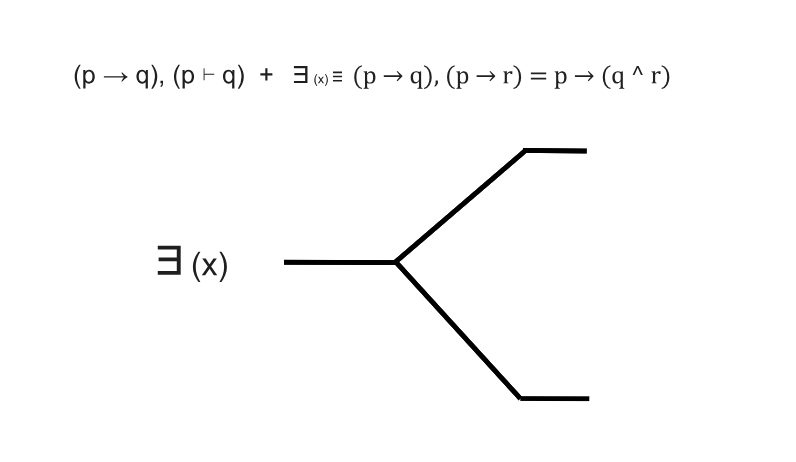
• Integral: Law of Identity

• Constant: Modus ponens

Derivative: existential quantifier

Flux Dimension

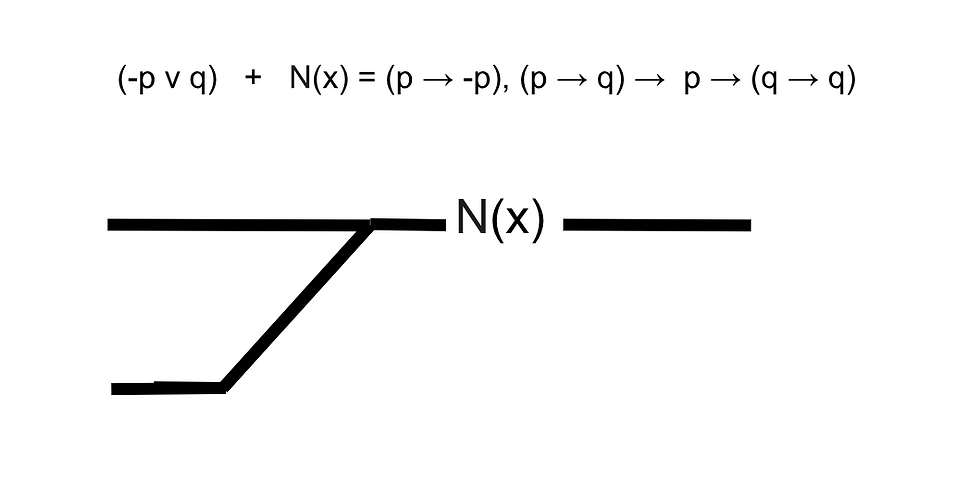
• Integral: Law of sufficient Reason

• Constant: Disjunctive syllogism

• Derivative: Negative quantifier

  
  

Existential Quantification and Modus Ponens

The relationship between modus ponens and the existential quantifier shows that when p implies q, and p exists, q naturally follows. For example, if dark clouds imply rain, then dark clouds automatically entail the idea of rain (vice versa). The existential quantifier (there exists an x such that p(x)) allows us to assert either state interchangeably. But note that the existential quantifier in ascribing x to p in p(x) in relation to an example such as 'rain' and/or 'dark clouds, is synthesizing the two in p(x), when you say dark clouds imply rain; more than inferring one from the other, you are 'joining' the latter to the former, creating/reestablishing the synthetic, dual construct.

Consider the Quranic verse:

وَكُنتُمْ أَمْوَٰتًۭا فَأَحْيَـٰكُمْ ۖ ثُمَّ يُمِيتُكُمْ ثُمَّ يُحْيِيكُمْ "

You were lifeless and He gave you life, then He will cause you to die and again bring you to life" (2:28)

This oscillation between states is further illustrated in Surah Ash-Sharh:

فَإِنَّ مَعَ ٱلْعُسْرِ يُسْرًا, إِنَّ مَعَ ٱلْعُسْرِ يُسْرًۭا "Surely with hardship comes ease. Surely with hardship comes ease" (94:5-6)

The Monothetic Dimension

In this dimension, objects are indicated through other objects. Nothing is 'individual' in the familiar sense (as the existential quantifier shows us); rather, the individual is what multiple things share. Bradley's regress exemplifies this:

If A relates to B through relation R:

• We need R1 to connect A to R

• We need R2 to connect R to B

• This chain continues infinitely

  
  

Example: "The book is on the table"

• Book (A) and table (B) are connected by "on" (R)

• But how is "on" connected to "book"?

• And how is "on" connected to "table"?

This concept appears in Surah Al-Ikhlas:

قُلْ هُوَ اللَّهُ أَحَدٌ اللَّهُ الصَّمَدُ لَمْ يَلِدْ وَلَمْ يُولَدْ وَلَمْ يَكُن لَّهُ كُفُوًا أَحَدٌ "

Say: He is Allah, the One and Only; Allah, the Eternal, Absolute; He begets not, nor is He begotten; And there is none like unto Him" (112:1-4)

Negative Quantification

Heisenberg captures this concept:

"In throwing dice, we do not know the fine details of the motion of our hands which determine the fall of the dice and therefore we say that the probability for throwing a special number is just one in six." (Werner Heisenberg 'Physics & Philosophy', Sec 11)

This principle appears in quantum mechanics but was grappled with by earlier philosophers. Descartes noted that the Infinite is apprehended directly, before finite things that seem easier to comprehend.

" How can finite grasp infinity ? " asks Dryden. He had already been answered by Descartes that however difficult to comprehend, the Infinite is known or apprehended directly and before the finite things which are easier to comprehend. (Samuel Alexander 'Space, Time & Diety', chp I)

The Flux Dimension

This dimension shows neither embodiment nor commonality, only transitions. We focus on:

• The procedure of states rather than states themselves (like turning the pages of a sketchbook)

• The flowing rather than the fixed

• What's "going on" rather than what "is"

  
  

These transitions follow the principle of least action -

A natural system will always move in a way that minimizes its action, following the path of least resistance between any two points. This is not merely economy of motion but a fundamental principle describing how nature optimizes all processes.

The Interconnected Universe

Each dimension borrows from and lends to others:

• Continuity requires monothetic identities and discrete states to showcase continuity

• The monothetic identities borrow from flux to define the difference (change) against which identity is asserted, and it requires continuity to show this procedure.

• Flux borrows from discreteness 'states' between which It can showcase transitions/flux, as well as monothetic identities whose components are those same states (there's otherwise no flux between discrete states, as it's only the common between states which the flux moves through)

• Discreteness borrows from monothetic identity 'identities' whose components it can discretize, and from flux the transitions that characterize the discretization process by which those identities unfold.

• As far as continuity is concerned, any 'process' whatsoever, is continuous insofar as its a 'certain process' and is distinguished by a procedural 'framework'.

  
  

Iman (إيمان) and Understanding

A major principle in islam is based on this function, ‘Belief’ or “Iman’, because, the idea here is that since, as Hiadagger notes, we’re ‘thrown’ in the world, subject to and surrounded by forces we don’t understand, situations and circumstances we didn’t choose, and that we mostly don’t understand what’s happening and most of what we know is happening, ‘Imaan’ appears as the antidote’ saying that in such situations, we must exercise faith: faith in the rationality of the world, that what seems a chaotic and ‘irrational’ world is governed by a rational force, a rationale whose complex workings we could only faintly intuit, but best yet confide our reason in, being that, as Borges put it

“for the machinery of the world is much too complex for the simplicity of men” (Inferno 1 32)

It’s not that the world is irrational, it’s that so much must be grasped by us before the world can make sense in the sense that we presuppose when we declare it irrational.

The fundamental incomprehensibility of the world, is part and parcel of being ‘in the world’. Iman rationalizes the irrational, and maintains that there’s a structure, but that such a structure, though could be comprehended through revelation; must still be founded on belief, and rest on it as the vehicle by which to navigate the uncertainties of the immediate, which, like negational quantification, is a mechanism by which we ‘defer’ judgement regarding the nature of the immediate, the not yet rational, but when we defer, we always ‘defer to’; namely, to something rational, such is the function of Iman. 

إيمان (Iman)

• Faith in the world's underlying rationality

• A mechanism for dealing with apparent chaos

• A framework for deferring judgment while maintaining rational hope